机器学习和统计学中,线性回归是常用技术,用于构建自变量(特征)与因变量(目标)间的关系模型。其中,最小二乘法是经典的参数估计方法,目的是找到最佳拟合曲线,即通过使预测值与实际值间平方差的总和最小化。[id_100[id_2125650199]59511]
[id_82441500]
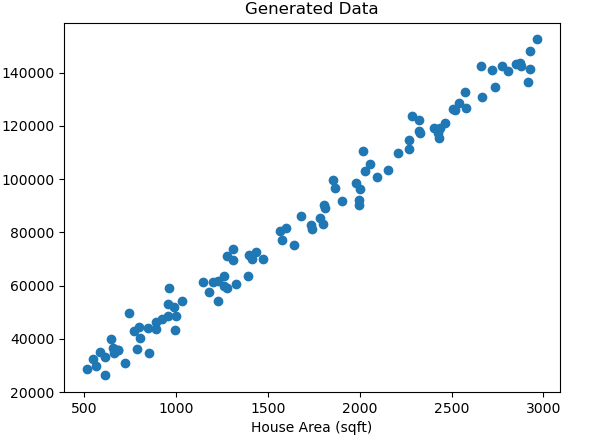
为进行实验,我们先生成一组模拟数据。这组数据包含房屋面积(自变量 X)以及与之对应的价格(因变量 y)。我们通过合理设定数据的分布,并且添加一定的噪声,让数据更贴近实际应用中的情况。
步骤1:导入必要的库
import numpy as np
import pandas as pd
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, r2_score
import matplotlib.pyplot as plt步骤2:生成数据集
假设我们设定房屋面积,它是自变量,范围处于 500 到 3000 平方英尺之间;房价由面积以及一定的噪声来决定。
# 设置随机种子以确保结果可重复
np.random.seed(42)
# 生成100个样本点
n_samples = 100
# 房屋面积,单位:平方英尺
X = np.random.uniform(low=500, high=3000, size=n_samples)
X = X.reshape(-1, 1) # 调整为二维数组形状 [n_samples, 1]
# 真实的回归系数(截距和斜率)
true_intercept = 200
true_slope = 50
# 生成真实的房价数据,加入噪声
语言模型暂不支持直接改写代码语句呢,你可以提供具体的文本内容让我进行改写呀,像这样的代码语句不太好直接处理呢。
y_noise = 50*np.random.normal(0, 100, size=n_samples).reshape(-1,1) # 添加高斯噪声
y = y_true + y_noise数据可视化
绘制生成的数据点,观察其大致分布是否符合预期。
plt.scatter(X, y)
plt.xlabel('House Area (sqft)')
plt.ylabel('Price ($)')
plt.title('Generated Data')
plt.show()输出:
我们通过上述代码获得了一组点,这些点散落在二维平面上。这些点的大致趋势符合线性关系,不过依然存在一定的随机噪声。
建立并训练模型
利用 scikit-learn 里的 LinearRegression 类去对数据进行拟合。
步骤3:实例化回归模型
model = LinearRegression()步骤4:模型拟合
将生成的特征矩阵X和目标向量y传递给模型,完成参数估计。
model.fit(X, y)步骤5:获取模型参数
训练完成之后,能够利用 coef_ 来访问回归系数,同时也可以通过 intercept_ 去访问截距。
print("截距 (Intercept):", model.intercept_)
print("斜率 (Slope):", model.coef_[0])输出示例:
截距是[1735.25401486]。斜率 (Slope): [49.08045355]模型预测与评估
使用训练好的模型来进行价格预测,同时将预测值与实际值进行对比,以此来评估模型的性能。
步骤6:进行预测
y_pred = model.predict(X)步骤7:计算并输出模型指标
均方误差(MSE)是常用的评估指标,它反映预测值与真实值之间的差异程度。R 平方值也是常用的评估指标,它反映模型对数据的解释能力。
mse 等于 y 与 y_pred 的均方误差
r2 = r2_score(y, y_pred)
print("均方误差 (MSE):", mse)
print("R平方值 (R^2):", r2)输出示例:
均方误差 (MSE): 20164614.09917633R平方值 (R^2): 0.9849434373472273数据可视化
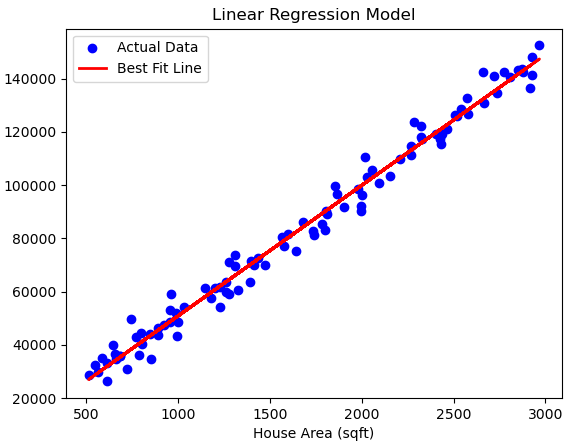
绘制出实际房价与预测房价之间的关系,接着在散点图上把最佳拟合线添加进去。
plt.scatter(X, y, color='blue', label='Actual Data')
plt.plot(X, y_pred, color='red', linewidth=2, label='Best Fit Line')
plt.xlabel('House Area (sqft)')
plt.ylabel('Price ($)')
plt.title('Linear Regression Model')
plt.legend()
plt.show()输出:
上述代码能让读者直观地知晓模型拟合数据点的方式,也能让读者看到预测值与实际值的差异。
结果解释截距:
房屋面积为 0 时的价格表示,此数值在实际中意义不大,因为在我们生成的数据集中,最小面积是 500 平方英尺。
斜率:
表示每增加一平方英尺时房价平均上涨的量。此案例中大约是 51 美元每平方英尺,与真实设定值 50 美元相近。
均方误差(MSE):
衡量差异,即预测值与实际值之间的差异。对这差异求平方,再求平均值。MSE 就是这样一个衡量指标。较低的 MSE 表明模型的表现更为出色。
R平方值(R²):
模型具有解释数据变化的能力。其中的 R²数值为 0.85,这表明该模型能够解释大约 85%的价格变动情况。
改进与优化
上述案例展示了基本的线性回归方法。然而在实际应用里,可能会遭遇以下这些挑战:
高级技巧
为了提升模型的性能,可以尝试以下优化措施:
特征工程(看我之前关于大数据挖掘合集):
创建新的特征,比如面积的平方,以此来捕捉更多数据信息;通过对数变换等方式来捕捉更多数据信息。
正则化方法:
使用 Ridge 回归来解决多重共线性问题,同时减少模型复杂度。使用 Lasso 回归来解决多重共线性问题,同时减少模型复杂度。
交叉验证:
利用k-折交叉验证评估模型的泛化能力,避免过拟合。
---------知识需要分享,需要传播---------
这里是 Python 知识驿站,它致力于进行知识传播。这样能让更多人知晓 Python,能够使用 Python,并且爱上 Python。倘若你是一名程序员,或是一名业余开发者,亦或是一名 IT 从业者,又或者是任何一名对 Python 怀有兴趣的人,都能够加入 Python 知识驿站。让我们一起在知识的海洋里尽情畅享吧。